DIVISONS

1. Intitulé

L’activité proposée permet, en fin de cycle trois comme en sixième, de travailler le concept de division aussi bien que les techniques opératoires. Objectif et mise en œuvre présentent des variations en fonction du niveau où l’activité est proposée.

2. Présentation de la séance

· Thème

Consolidation des acquis de la division euclidienne pour tous et découverte de la division décimale pour les 6°

· Extraits du programme officiel

• Programme de cycle 3

Division euclidienne de deux nombres entiers (quotient entier et reste)

• Programme de 6°

2.2 Division, quotient Division euclidienne [Programme cycle 3 ; document d™application, p. 25 à 29]

- Reconnaître les situations qui peuvent être traitées à l'aide d'une division euclidienne et interpréter les résultats obtenus. - Calculer le quotient et le reste d'une division d'un entier par un entier dans des cas simples (calcul mental, posé, instrumenté). - Connaître et utiliser le vocabulaire associé (dividende, diviseur, quotient, reste).

Division décimale

- Calculer une valeur approchée décimale du quotient de deux entiers ou d'un décimal par un entier, dans des cas simples (calcul mental, posé, instrumenté).

A l'école élémentaire, les décimaux ont pu intervenir dans des problèmes de division au delà de la virgule (partage d'une longueur par exemple), mais aucune compétence technique n’a été mise en place. La division décimale permet d'obtenir soit la valeur décimale exacte (quand elle existe), soit une valeur décimale approchée du quotient. Ce qui est indiqué concernant l’extension de la notation au cas de deux décimaux permet d’aborder le calcul d’un quotient de deux décimaux, sans qu’aucune compétence ne soit exigible à ce sujet

· Objectifs de l’activité

Cette activité est proposée dans son intégralité en sixième alors que la partie « Mais vraiment quelle chance » ne sera pas abordée en CM2.

En CM2 : cette activité permet un réinvestissement des notions étudiées avec des « grands nombres ».

En 6° : cette activité permet de revoir le vocabulaire, la technique opératoire (uniquement calcul posé), le sens, l’utilisation dans des problèmes et des propriétés liées à la division euclidienne pour la partie commune ; le dernier problème permet d’aborder la division décimale.

• Niveau de réalisation – Situation dans la progression annuelle

En CM2 : cette activité se situe en fin d’apprentissage de la division euclidienne.

En 6° : la multiplication des nombres décimaux aura été traitée.

· Type de séquence – Nombre de séances

En CM2 : une séance d’environ 1h30 est nécessaire avec temps de recherche personnelle et mises en commun avec la classe.

En 6° : pour la partie « commune », il faut prévoir une 1h (même type de déroulement qu’au CM2). Il faudra une quinzaine de minutes pour la partie uniquement pour les 6° quelques séances plus tard (introduction de la division décimale).

• Gestion de la classe

La séance se déroule en classe entière .Le travail de recherche est individuel.

Les élèves n’utilisent pas la calculatrice et travaillent directement sur la fiche ou sur leur cahier d’exercices pour certains calculs à poser.

Chaque séance a été animée par l’enseignant de sa classe mais elle a été suivie également par un enseignant ou deux enseignants (du CM2 et de 6°)

3. Descriptif détaillé de la séquence

• Document extrait du manuel « Dimathème, Didier édition 2000 », point de départ de l’activité :

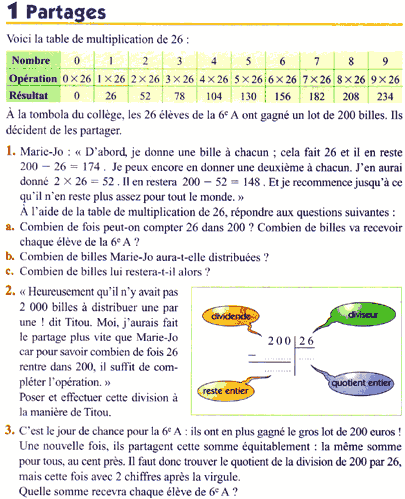
• Document proposé aux élèves

• Document commun aux CM2 et aux 6° :

Activité «Une classe très chanceuse »

A la tombola du collège, les 26 élèves de la classe de 6°C ont gagné un lot de 195 billes. Ils décident de les partager.

I. Stéphanie veut faire le partage en donnant une bille à chacun et recommencer jusqu’à ce qu’il n’en reste plus assez pour tout le monde.

Aide-la en répondant aux questions suivantes (n’oublie pas la table de multiplication !):

1. Combien de fois peut-on compter 26 dans 195 ?

Combien de billes va recevoir chaque élève de 6°C ?

2. Compléter les pointillés :
• 26×……...< 195 < 26×………. .
• ………….< 195 <……………. .
3. Combien de billes Stéphanie a-t-elle distribuées ?
4. Combien de billes lui reste-t-il ?

II. Bastien dit : « Heureusement qu’il n’y avait pas 3000 billes. Je vais plus vite que Stéphanie en complétant l’opération suivante : »

Effectue cette opération :

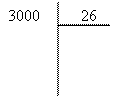
Compléter :

Bastien et toi venez d’effectuer une …………………………

3000 est le ……………………., 26 est le ……………………, …….est le quotient entier et

……………..est le reste entier.(On remarque que ce reste ….est plus ………..que le …………………)

III. A toi de jouer :

1. Effectue les divisions suivantes à la manière de Bastien:

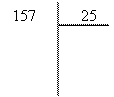
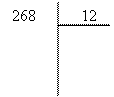
2. Pose et effectue les divisions suivantes :

584 : 20 632 : 7

Quelle opération utile !

1. Aujourd’hui, il y a 318 élèves qui mangent à la cantine. Pour le dessert, chacun aura un gâteau.

Les gâteaux se vendent par paquet de 28.

Combien doit-on prévoir de paquets ?

2. Un fabricant de disques compacts expédie 971 disques à un client. Les disques sont emballés dans des boîtes. Chaque boîte contient 28 disques.

La dernière boîte n’est pas pleine.

Combien a-t-on mis de disques dans cette boîte ?

• Document uniquement pour les 6° :

Mais vraiment, quelle chance !

C’est vraiment le jour de chance pour la 6°C : ils ont gagné le gros lot 195 euros !

Ils doivent, à nouveau, partager cette somme de façon équitable : la même somme pour tous.

Il faut donc trouver le quotient de la division de 195 par 26, mais cette fois avec 1 ou plusieurs chiffres après la virgule.

Quelle somme exacte recevra chaque élève de 6°C ?

• Remarques par deux enseignants de 6°(après discussion avec un enseignant du CM2)

Nous avons d’abord remarqué, globalement, une différence dans l’appropriation du travail par les élèves, une différence de rythme (un enseignant de CM2 a laissé presque 30min en autonomie alors que nous « recadrons » les recherches au bout d’un quart d’heure maximum par exemple), du vocabulaire employé et des précisions données au cours des corrections (méthodes d’auto-vérification par exemple -calcul du nombre de chiffres au quotient-)

A la suite des différentes discussions, il a semblé nécessaire de modifier la division du II , c’est-à-dire de proposer une division où la méthode de la première partie serait longue et fastidieuse, mais autre que celle posée, le lien entre les parties I et II n’ayant pas était toujours fait par les élèves. (Proposition : 300026, en liaison avec la remarque de Bastien .)

Dans la partie III, le problème qui est apparu, mais globalement dans les deux niveaux, a été sur l’opération 6327, lorsqu’il a fallu mettre un « zéro » aux unités du quotient avant de mettre la virgule.

Dans la partie « Quelle opération utile », dans le problème 2, globalement tous les élèves ont posé la division, beaucoup dans les 2 niveaux ont eu le résultat juste. Mais, comme prévu, les difficultés ont été dans la capacité à interpréter les résultats, en particulier pour le premier problème où il fallait ajouter 1 au quotient entier pour répondre à la question posée (sérieux problèmes pour certains CM2).

C’est la version modifiée après ces remarques qui est proposée.